Прогрессивный рост
Содержание:
- Сложные проценты по вкладу
- Общая формула расчета процентов по вкладу
- Обратная задача на проценты
- Простые и сложные проценты
- Сложные проценты в примерах
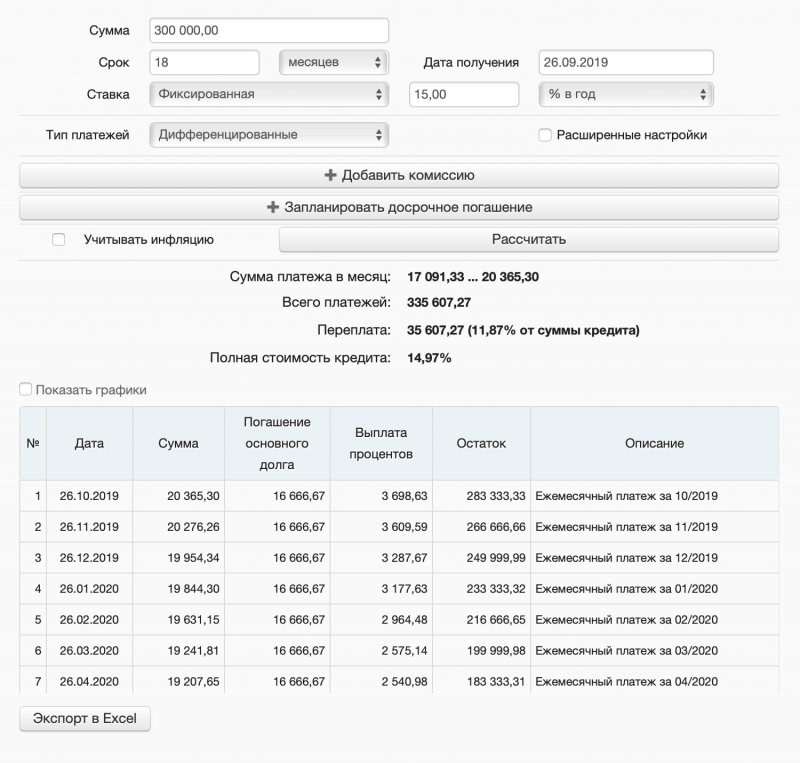
- Как рассчитать общую сумму переплаты по кредиту
- Периодичность начисления процентов
- Простые проценты в математике
- Расчет банковской процентной ставки
- Школьные задачи на сложные проценты
- Литература
- Пример
Сложные проценты по вкладу
Отличие простых процентов от сложных на самом деле довольно большое. При выборе депозитного продукта наверняка каждому приходилось слышать о таком понятии, как капитализация. То есть это та схема начисления прибыли, при которой начисленная прибыль причисляется к телу депозита, а на него в будущем снова начисляется доход.
Отсюда можно сделать вывод, что капитализация позволяет получить большую прибыль по сравнению с простым процентом. Чтобы наглядно в этом убедиться рассмотрим формулу расчета сложных процентов, а выглядеть она будет следующим образом: B=(K?H?P/N)/100, где:
- B – размер начисленной прибыли;
- K – тело депозита;
- H – годовая ставка;
- P – количество дней, в течение которых происходит капитализация;
- N – число дней в году.
Чтобы наглядно понять, как именно будет рассчитываться сложный процент. Рассмотрим простой пример. Сумма депозита 50000 рублей процентная ставка в год 7%, капитализация осуществляется ежемесячно, срок действия договора один год. Произведем расчет прибыли за первый месяц пользования депозитом: B=(50000?7?30/365)/100=287,6 рублей – это прибыль за первый месяц. В следующем периоде расчет будет выглядеть следующим образом: B=(50287,6?7?31/365)/100=298,9 рублей.
Из вышеприведенного примера можно сделать вывод, что капитализация позволяет получать с каждым месяцем большую прибыль по сравнению с предыдущим
Вот только при выборе депозитного предложения обязательно обратить внимание, с какой периодичностью осуществляется капитализация процентов, чем чаще, тем больше выгоды получает клиент
Общая формула расчета процентов по вкладу
Использование формулы простых процентов целесообразно в случае начисления процентов в конце срока размещения депозита или если они будут переводиться на отдельный счет – если капитализация договором не предусмотрена.
Если средства размещаются на длительный срок и сумма большая, банк использует формулу простых процентов: сумма дохода с процентов занижается.
В этом случае используется формула следующего вида:
S = (P x I x t / K) / 100
Обозначения:
S – конечная сумма, полученная по завершению действия депозита;
P – сумма изначально внесенная на депозит;
I – размер % ставки (за год);
t – кол-во дней начисления %;
K – кол-во дней за год по календарю.
Для расчета сложных процентов, которые применяются в случае капитализации в течение всего периода действия депозитного договора (каждый месяц, раз в квартал, ежедневно), нужно применить следующую формулу:
S = (P x I x j / K) / 100
Эти символы имеют следующее значение:
I – % ставка за год;
J – сумма дней по календарю за конкретный период, на протяжении которого финансовое учреждение капитализирует проценты, начисляемые по выбранному виду вклада;
К – количество дней в году по календарю;
P – изначально привлеченная сумма для размещения на вкладе, в дальнейшем это будет сумма, в которую уже учитываются капитализированные процентные начисления;
S – сумма, которая должна быть выплачена клиенту финучреждения, в ней уже учтены капитализированные %.
Обратная задача на проценты
Обратной задачей на проценты называют такую, в которой за неизвестные выступают количество лет или процентная ставка.
Задача 2. Вкладчик взял в кредит 3000 рублей и должен вернуть через пять лет. Найти процентную ставку кредита, если известно, что нужно отдать банку 8100 грн.
Решение: Выведем формулу для этой задачи.P=P*(1+n/100*r); P/P=1+n/100*r; n= (P/P-1)/r*100.Выполняем вычисления по выведенной формулеn= (8100/3000-1)/5*100=1,7/5*100=34 (%). Следовательно, процентная ставка кредита составляет 34 %. Если в обратной задачи на проценты нужно найти количество лет, то нужная формула на основе предыдущих выкладок будет выглядетьr= (P/P-1)/n*100
Простые и сложные проценты
Инвесторы, которые работают на рынке Форекс, сталкиваются с повторным вложением денег (реинвестированием) постоянно. Если банковские депозиты приносят владельцам прибыль через несколько месяцев или даже год, то на валютном рынке прибыль/убыток появляется после каждой сделки.
Поэтому все, кто интересуется инвестициями на Форексе, будут регулярно работать с простыми и сложными процентами. Давайте же разберемся, что же означают эти понятия.
Простой процент используется в случаях, когда база начисления процентов всегда равна начальной сумме вложений. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.
Каждый раз, когда инвестор хочет несколько раз «прокрутить» свои деньги через инвестиционный инструмент, он сталкивается со сложным процентом. Полученная прибыль на первом круге реинвестируется и проценты уже начисляются на более крупную сумму.
В инвестициях на рынке Форекс сложный процент используется постоянно, потому что сумма вложений меняется после каждой сделки. Многие инвесторы используют тактику «вложил и забыл», оставляя полученную прибыль работать вместе со стартовым вкладом.
Разница между простыми и сложными процентами на первый взгляд кажется не такой уж большой. Но чем больше проходит времени, тем очевиднее становится преимущество сложных процентов:
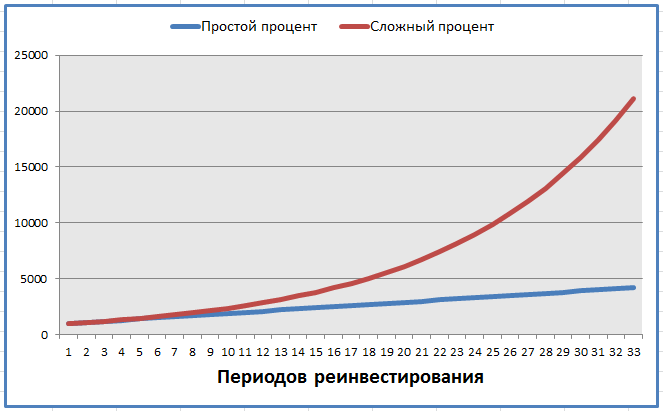
Простые и сложные проценты на одном графике
Конечно, это всё теория и на практике добиться 30-кратного реинвестирования прибыли совсем непросто. Но факт остаётся фактом — сложные проценты могут сослужить хорошую службу инвестору. И чтобы умело их использовать, нужно правильно их считать, в чём помогут несколько полезных формул.
Сложные проценты в примерах
Что такое сложные проценты и как их правильно считать?
Выглядит это так: конечная сумма равна начальной, умноженной на сумму единицы и числа равного процентной ставке деленной на 100, в степени равной периоду на который осуществляется вложение (конечная сумма = начальная сумма * (1 + %)n).
В качестве примера не найти ничего лучшего, чем вклад денег на срочный депозит. В реальности для расчета сложных процентов по вкладам банкиры, применяют совершенную формулу имеющую вид: конечная сумма равна, начальной умноженной на единицу плюс процентная ставка деленая на 100, умножить на количество дней, деленное на количество дней в году, все в степени равной периоду вклада (конечная сумма = начальная сумма * (1 + p*d/y)n.
Другими словами, если вы вложили 1000 рублей под 12% годовых, то через год вы получите 1120 рублей. Если на второй год вы продлите вклад не с 1000 рублей а с 1120, то вместо 120 рублей вы уже получите 134,4 р. Кажется не большая разница, но вот что будет за 50 лет:
- Через З года — 1400
- Через 4 года — 1570
- Через 10 лет — 3100
- Через 20 лет — 9640
- Через З0 лет — 29 960
- Через 40 лет — 93 050
- Через 49 лет — 258 040
- Через 50 лет — 289 000
Однако все познается в сравнении и чтобы в полной мере оценить могучий потенциал того, что называется реинвестированием, необходимо сравнить, какие же результаты дают простые и сложные проценты. Если простые проценты дают линейный прирост прибыли, то реинвестиции – это экспоненциальное увеличение капитала, которое тем сильнее, чем большая сумма под больший процент и на дольший срок была вложена.
При необходимости из указанной выше формулы по расчету сложных процентов по банковским вкладам легко выводятся и формулы для определения других необходимых величин: действующей процентной ставки ((конечная сумма/ начальную сумму)1/n – 1); периода, за который из имеющейся суммы потребуется получить искомую (n = log(1+процентная ставка) (конечная сумма / начальную сумму)).
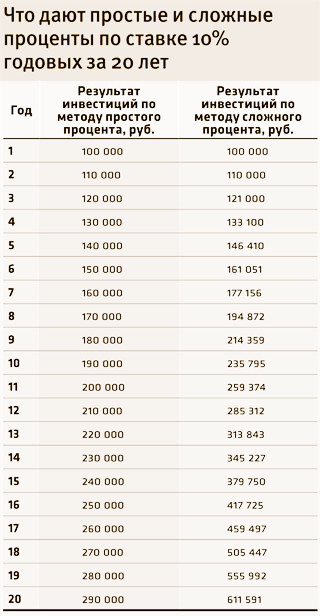
Все бы было здесь прекрасно, если бы не одно «но» – для того, чтобы сложные проценты действительно раскрыли свой полный потенциал и начали наращивать хорошую прибыль, требуется довольно продолжительный срок либо очень высокая процентная ставка, что в честных проектах встречается крайне редко.
А вот пример того, как можно заработать 1 миллион долларов за 11 лет, при условии первоначального вклада три тыс. долларов по 50% годовых, и ежемесячно нужно докладывать по 300 долларов (3600 в год):
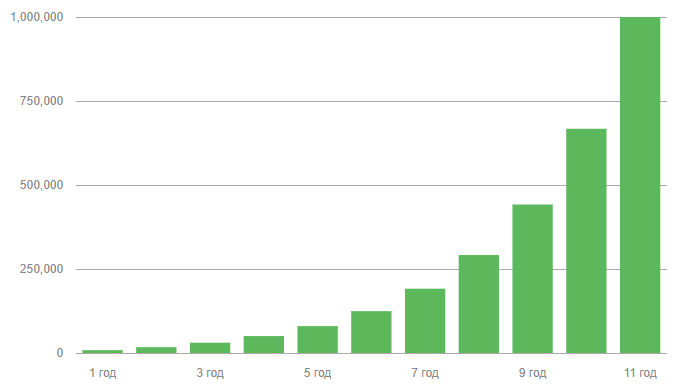
1 год $8 565
2 год $17 362
3 год $30 558
4 год $50 351
5 год $80 042
6 год $124 577
7 год $191 381
8 год $291 586
9 год $441 893
10 год $667 355
11 год $1 001 032
Более подробно данный пример описан в статье про пассивный доход, там же вы найдете много способов и примеров пассивных инвестиций.
Опрос: Как вы поступаете с прибылью от инвестиций?
Poll Options are limited because JavaScript is disabled in your browser.
Эйнштейн о сложных процентах
Альберт Эйнштейн называл сложные проценты величайшим изобретением человечества. Об этом часто упоминают мотивационная литература и всякого рода финансовые консультанты. Также они любят приводить пример, что если положить $1 на депозит под 20% годовых с капитализацией процентов и каждый день вносить на счет еще по доллару, то всего через 32 года вы будете обладать миллионом.
Однако на данный момент 20% в год по вкладу вам дадут только мошенники. В России банки предлагают по долларовым депозитам до 4%. Чтобы сегодня накопить миллион долларов по такой красивой схеме, необходимо около 120 лет.
Сложные проценты – это мощный рычаг мировой финансовой системы для преумножения прибыли, который может быть использован любым, неважно, дивидендный ли это инвестор или вкладчик валютных депозитов, присмотревшись вокруг можно заметить, что именно реинвестиции являются той самой «волшебной печатной машинкой», которая при правильной настройке может в неограниченном количестве создавать деньги из воздуха. И позиция сторонников, и позиция критиков реинвестирования содержит свои разумные аргументы, что выбрать: снимать или добавлять к вкладу прибыль, каждый пусть решает сам, единственное, что необходимо всегда, так это четко понимать, что и зачем ты делаешь, принимая на себя всю ответственность за свои поступки
И позиция сторонников, и позиция критиков реинвестирования содержит свои разумные аргументы, что выбрать: снимать или добавлять к вкладу прибыль, каждый пусть решает сам, единственное, что необходимо всегда, так это четко понимать, что и зачем ты делаешь, принимая на себя всю ответственность за свои поступки.
Как рассчитать общую сумму переплаты по кредиту
Стоит помнить, что итоговая сумма переплаты напрямую влияет на конечный остаток задолженности. Например, если заемщик будет регулярно вносить немного больше средств, чем расписано по графику платежей, то переплата также уменьшится. На сумму переплаты влияет и срок кредитования (чем он меньше, тем уменьшается величина переплат). Ног стоит понимать, что кредитные организации, оформляя ссуды, преследуют цель получения выгоды, поэтому отыскать банк, который кредитует население с нулевыми переплатами невозможно.
Формула простых процентов
Формула расчета простых процентов легко применима для просчета общей итоговой переплаты. Использовать ее может каждый потенциальный займополучатель. Для этого предварительно следует вооружиться следующими цифрами:
- Использовать общую сумму ссуды. Например, 500 000.
- Узнать стоимость одного процента: 500 000/100=5 000.
- Перемножить величину процента на установленную ставку (допустим, размер годовых 18%): 5 000х18%=45 000 (годовая переплата).
Итоговый результат и становится показателем суммы переплаты. Если ссуда оформлена на несколько лет, то 45 000 следует умножить на их количество, чтобы высчитать общую переплату по всему периоду кредитования. Такая нехитрая формула начисления простых процентов поможет проанализировать предложения различных кредиторов и выбрать оптимальные под себя условия.
 Расчет простых процентов
Расчет простых процентов
Расчет сложных процентов
Но не стоит забывать, что при оформлении займа, плательщик может столкнуться и с различными дополнительными взиманиями (за сборы, допуслуги, комиссионные, оформление и обслуживание ссуды). Такое встречается уже редко среди банков, но можно столкнуться и с такой процедурой кредитования. В данном случае при расчете полной переплаты следует учитывать и все дополнительные банковские сборы. Например, при годовой чистой переплате в 45 000, с учетом дополнительных взиманий (например, 2 500) переплата становится уже 47 500.
 Расчет сложных процентов
Расчет сложных процентов
Периодичность начисления процентов
Проценты по банковским депозитам должны выплачиваться клиенту по его требованию ежеквартально обособленно от суммы самого депозита, а невостребованные начисленные проценты автоматически увеличивают сумму вклада (ст.839 ГК РФ). Однако, договорами может быть предусмотрен иной порядок: в зависимости от выбранного банковского продукта проценты выплачиваются каждый месяц, квартал, полугодие или по окончанию срока действия соглашения.
Как начисляются проценты. В соответствии с Гражданским кодексом РФ дополнительный доход в виде процентов по договорам банковского вклада начинает начисляться со следующего дня после размещения денежных средств на депозитном счете и до дня возврата финансовых активов клиенту. Если списание средств осуществляется до окончания срока действия договора, то начисление процентов осуществляется до дня списания включительно.
При начислении процентов без учета капитализации сумма предполагаемого дохода вычисляется по формуле:
Sp – размер получаемой от размещения средств дополнительной прибыли
P – вложенные личные денежные средства клиента
I – годовая процентная ставка в зависимости от типа вклада
t – количество календарных дней, за которые будут начисляться проценты
K – количество дней в году.
Если, например, внести 15000 рублей на 5 месяцев под 10%, то доход клиента составит: 15000 * 150 * 0,10 / 365 = 616 рублей 44 копейки.
Как считать «сложные проценты». При капитализации процентов по вкладу каждый следующий месяц проценты начисляются не только на основные личные средства клиента, но и на процент, начисленный в прошлых периодах. Формула для расчета «сложных» процентов выглядит следующим образом:
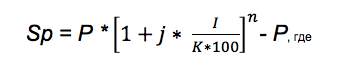
Sp – размер получаемой от размещения средств дополнительной прибыли
P – вложенные личные денежные средства клиента
I – годовая процентная ставка в зависимости от типа вклада
j – количество календарных дней в том периоде, за который будет осуществляться капитализация процентов
K – количество дней в году
n – число совершенных операций по капитализации процентов за весь срок действия банковского договора.
Практический пример. Клиент заключил с банком договор на размещение денежных средств в размере 15000 рублей на депозите на 5 месяцев под 10% годовых. По договору автоматически осуществляется капитализация процентов, которые начисляются ежемесячно. В этом случае число совершенных операций по капитализации процентов за весь срок действия банковского договора составит 5 раз, а количество календарных дней в том периоде, за который будет осуществляться капитализация процентов составит 30.
|
Месяц |
P |
I |
t |
Sp |
|
1 |
15000 |
10 |
31 |
127,40 |
|
2 |
15127,40 |
10 |
28 |
116,05 |
|
3 |
15243,45 |
10 |
31 |
129,46 1 |
|
4 |
15372,91 |
10 |
30 |
126,35 |
|
5 |
15499,26 |
10 |
31 |
131,64 |
|
630,90 |
Простые проценты в математике
Задача 5. В класс закупили 3 энергосберегающие окна, которые на 20 % дороже обычных. Сколько потратили денег, если за обычные окна нужно заплатить 1400 гривен.
Решение: Найдем цену энергосберегающего окнаP=1400*(1+20/100)=1680 (грн.) За три окна заплатили1680*3=5040 (грн).
Задача 6. В бочке объемом 200 литров перевозили масло . На станции отлили 60 литров. Сколько процентов от обьема осталось?
Решение: Задача состоит в нахождении количества в процентах масла от общего объема бочки.200-60=140 (л); 140/200*100%=70 % Осталось 70% объема бочки.
Задача 7. При несвоевременной уплате долгов насчитывают 2% пени за каждый просроченный день. Какую сумму нужно заплатить через 12 дней после срока погашения 500 рублей долга?
Решение: По формуле простых процентов находимP=500*(1+2/100*12)=620 (рублей)Нужно заплатить 620 рублей.
Рассмотрим задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир « Аглгебра ». (Номер в скобках)
Задача 8. (542) К сплаву массой 600 г, содержащему 12 % серебра, добавили 60 г серебра. Какое содержание серебра в новом сплаве?
Решение: Определяем сколько грамм серебра в первом сплавеP=600*12/100=72 (г)К найденному значению добавляем 60 грамм серебра P1=72+60=132 (г) При определении процентного содержания серебра не следует забывать, что вес нового сплава вырос на массу серебра, которую добавили. Если би Вы вычисляли следующим образом 132/600*100%=22% то получили — неправильный результат .ЗАПОМНИТЕ: в подобных задачах сначала находят меру ( вес, объем, длину) нового объекта, а затем находят содержание. В заданной задачи новый сплав получит массуP2=600+60=660 (г) а процентное содержание серебраP1/P2*100%=132/660*100%=20 % будет следующим — 20%.
Задача 9. (543) В саду росли яблони и вишни, причем яблони составляли 42% всех деревьев. Вишен было на 48 деревьев больше, чем яблонь. Сколько деревьев росло в саду?
Решение: К правильному ответу можно идти несколькими способами. Рассмотрим следующий из них. Пусть яблони составляют 42% всех деревьев, тогда вишни100-42=58%. Вишен на 48 больше нежели яблонь. Разница между ними в процентах составляет58-42=16% а в количестве — 48 деревьев. Задача состоит в нахождении количества деревьев, поэтому складываем отношения16% – 48 деревьев 100 % –Х деревьев Отсюда находим количество деревьев в садуХ=100*48/16=300 (деревьев).
Задача 10. (544) За два дня был проложен кабель. За первый день проложили 56% кабеля, а за другой — на 132 м меньше, чем первого. Сколько всего метров кабеля было проложено за два дня?
Решение: Задача похожа на предыдущую. За второй день проложили 100-56=44% кабеля, разница между первым и вторым днем составляет 56-44=12% и составляет 132 метра. На основе этого составляем отношение12% – 132 м100 % –Х м Отсюда находим искомую длинуХ=100*132/12=1100 (м.) За два дня проложили 1100 м.. кабеля.
Задача 11. (545) За первый день мальчик прочитал 25% всей книги, за второй — 72% от количества страниц что осталась, а за третий — остальные 84 страницы. Сколько страниц в книге?
Решение: 72 % процента от остатка книги составляет72*(100-25)/100= 54%. На третий день оставалось прочитать100-25-54=21% или 84 страницы. Составляем соотношение21% – 84 ст 100 % –Х ст с которого находимХ=100*84/21=400 (ст), что книга содержит 400 страниц.
Расчет банковской процентной ставки
Перед подписанием кредитного договора желательно понимать, какие суммы придется выплачивать, поэтому важен правильный расчет банковской процентной ставки. Многие онлайн-банки предлагают на своих сайтах заемщику калькулятор для этих расчетов, но на самом деле применить его не так и просто, но возможно сделать приблизительный расчет.
Многие методы расчета банковской процентной ставки сложны и требуют математических знаний. Поэтому остановимся на более простых способах. Если сложить все предложенные в списке платежи, то можно посчитать приблизительный процент, который придется выплатить за заемные средства:
- процент по кредиту;
- все комиссии банка (за рассмотрение заявки, открытие, обслуживание счета и так далее);
- все услуги по страхованию жизни и другие;
Для правильного расчета следует учитывать разные обстоятельства, которые могут возникнуть в момент пользования заемными деньгами, например, досрочное погашение, пени, штрафы и многое другое.
Некоторые клиенты банка, наоборот, доверяют кредитной организации на хранение свои финансы. Банк за это выплачивает процент, зависит его размер от многих факторов.
Школьные задачи на сложные проценты
Например, возьмем задачи из учебника для 9 класса авторов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир «Аглгебра». (Номер в скобках)
Задача 1. (556) Костюм стоил 600 грн. После того как цена была снижена дважды, он стал стоить 432 грн., Причем процент снижения второй был в 2 раза больше, чем в первый раз. На сколько процентов каждый раз снижалась цена?
Решение: Для упрощения вычислений обозначим X – первая скидка; X/2 – вторая скидка. Для вычисления неизвестной X составляем уравнение Упрощаем, и сводим к квадратному уравнению и решаем Первый решение не имеет физического смысла, второй учитываем при вычислениях. Значение 0,2 соответствует снижению на 0,2*100%=20% после первой скидки, и X/2 =10% после второй скидки.
Задача 2. (557) Определенный товар стоил 200 грн. Сначала его цену повысили на несколько процентов, а затем снизили на столько же процентов, после чего стоимость его стала 192 грн. На сколько процентов каждый раз происходила смена цены товара?
Решение: Поскольку проценты одинаковы, то обозначаем изменении цены товара через X. На основе условия задачи получим уравнение Его упрощение приведет к решению уравнения откуда корни приобретут значений Первая значение отвергаем, оно меняет суть задачи (сначала имеем снижение, а затем рост процентов, противоречит условию). Второе при пересчете составит 0,2*100%=20% процентов.
Задача 3. (558) Вкладчик положил в банк 4000 грн. За первый год ему начислена определенный процент годовых, а второго года банковский процент увеличен на 4%. На конец второго года на счете стало 4664 грн. Сколько процентов составила банковская ставка в первый год?
Решение: Обозначим через X – увеличение вклада в первый год, тогдаX+4/100%=X+0,04 начисления во второй год. По условию задачи составляем уравнение для определения неизвестной X После упрощений получим квадратное уравнение вида Вычисляем дискриминант и корни уравнения Первый корень отбрасываем, второй соответствует ставке в 6% годовых.
Задача 4. (564) В сосуде 12 кг кислоты. Часть кислоты отлили и долили до прежнего уровня водой. Затем снова отлили столько же, как и в первый раз, и долили водой до прежнего уровня. Сколько литров жидкости отливали каждый раз, если в результате получили 25-процентный раствор кислоты?
Решение: Обозначим через X – часть кислоты, которую отливали. После первого раза ее осталось 12-X, а процентное содержание кислоты После второй попытки содержание кислоты в сосуде составило. Разведя водой до 12 кг, процентное содержание составляло 25%. Составляем уравнение Упрощаем проценты и избавляемся знаменателей Решаем квадратное уравнение Условии задачи удовлетворяет второе решение, а это значит, что каждый раз отливали 6 кг жидкости. На этом знакомство со сложными процентами завершается. На практике Вам встретятся как простые так и сложные задачи. При проблемах с вычисления сложных процентов обращайтесь к нам, мы поможем Вам в решении задач.
Литература
- Джон К. Халл. Глава 4. Процентные ставки // Опционы, фьючерсы и другие производные финансовые инструменты = Options, Futures and Other Derivatives. — 6-е изд. — М.: «Вильямс», 2007. — С. 133—165. — ISBN 0-13-149908-4.
- Джереми Миллер. Правила инвестирования Уоррена Баффетта = Jeremy Miller: Warren Buffett’s Ground Rules: Words of Wisdom from the Partnership Letters of the World’s Greatest Investor. — М.: Альпина Паблишер, 2017. — 374 с. — ISBN 978-5-9614-6212-8.
- Нечаев В. М., Яроцкий В. Г. Процент, в экономике и с юридической точки зрения // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Пример
Хорошей иллюстрацией является известная евангельская притча о том, как одна бедная вдова во времена Иисуса Христа принесла в жертву в храм последнее, что у неё было — две самых мелких монеты, лепты. Если представить себе, что в то время существовали банки, и она внесла бы одну монетку в банк, то какая сумма накопилась бы на банковском счёте к сегодняшнему дню, учитывая, что банк обеспечивает капитализацию процентов в сумме, скажем, пять процентов годовых?
Последующие расчёты как раз и иллюстрируют применение сложных процентов. Нам[кому?] легче будет говорить, не о лепте, а о копейке. Если ставка составляет 5 % годовых, то после первого года хранения капитал составил бы копейку плюс 5 % от неё, то есть возрос бы в (1 + 0,05) раза. На второй год 5 % рассчитывались бы уже не от одной копейки, а от величины, большей её в (1 + 0,05) раза. И, в свою очередь, данная величина увеличилась бы тоже за год в (1 + 0,05) раза. Значит, по сравнению с первичной суммой вклад за два года возрос бы в (1+,05)2{\displaystyle (1+0,05)^{2}} раз. За три года — в (1+,05)3{\displaystyle (1+0,05)^{3}} раз.
К 2016 году первичный вклад вырос бы до величины в (1+,05)2016{\displaystyle (1+0,05)^{2016}} раз больше первоначальной. Величина (1+,05)2016{\displaystyle (1+0,05)^{2016}} составляет 5,22⋅1042{\displaystyle 5,22\cdot 10^{42}}. При первоначальном вкладе в одну копейку к 2012 году сумма составит 5,22⋅1040{\displaystyle 5,22\cdot 10^{40}} рублей, то есть свыше 52 додециллионов.
Первоначальная идея применения к старинной притче оценок в сложных процентах принадлежит польскому математику Станиславу Ковалю и опубликована им в начале семидесятых годов в книге «500 математичных загадок».
Точная формула для оплаты ежемесячно
Точная формула для ежемесячного платежа
C=Pr(1−1(1+r)n){\displaystyle C=Pr/(1-1/(1+r)^{n})}
с = ежемесячный платеж
P = начальная сумма
r = ежемесячная процентная ставка
n = количество периодов выплат
Периодическое начисление
Функция суммы сложных процентов является экспоненциальной функцией с точки зрения времени.
P(t)=P(1+rn)nt{\displaystyle P(t)=P_{0}(1+{r \over n})^{nt}}
t = Общее время в годax
n = число периодов наращения в год
г = Номинальная годовая процентная ставка выражается в виде десятичной дроби. 6 т.д .:% = 0,06
nt = означает, что nt округляется до ближайшего целого числа.
Непрерывное начисление
Пределом (1+rn)nt{\displaystyle (1+{r \over n})^{nt}} при n→∞{\displaystyle n\rightarrow \infty } является ert{\displaystyle e^{rt}} (см. E (число)), таким образом, для непрерывного начисления, формула принимает вид:
P(t)=Pert{\displaystyle P(t)=P_{0}e^{rt}}